1.4 The economics of multiplexes
 
The previous sections surveyed the existing state of knowledge on the multiplexes and their impact in the European exhibition sector. The empirical evidence from the LE/BIPE survey has confirmed the importance of numerous issues, such as the impact of screen density, discussed in Section 1. In this section, we consider some strategic aspects of multiplex operations from an economic point of view.
 
There are a number of features of demand for cinema which are important in understanding the advantages associated with multi-screen cinemas. We focus on three features, using economic models. The three models are treated independently of one another, so as to focus on one issue at a time. All three models focus on the effect of having many screens, in terms of capturing existing demand for films and cost economies. The models do not go into the possibility that multiplexes generate new demand, for example by providing free parking, or by giving customers a second choice if their first choice film is sold out. The following sections present each model, the dynamic demand model is discussed in greater detail (see Model 1), while the other two models are summarised very briefly (see Models 2 and 3).
 
 
Model 1: Dynamic Demand for Films
 
New films are released at different dates and at any one time there will be many films shown in cinemas. A number of them will be in their first week of release; others will be well through their release. Films also differ by type: there are blockbusters, less popular mainstream films, art-house films and repertory films. By having more than one screen on the same site, the cinema can show more than one film at a time, thereby attracting larger audiences. The other possibility is to build other cinemas, but there are clearly economies of scale in building them on the same site: these economies are exploited fully in a purpose-built multiplex where the screens are set out so that a single projection room can serve all the screens.
 
If a cinema with more than one screen is being built, or if an existing single screen cinema is to be refurbished to include more screens, two questions naturally arise: what is the optimum number of screens to build, and how many people should each one hold?
 
In order to investigate these questions, we begin with a simple model of demand and supply of exhibition of in a small town. An entrepreneur is considering building one or more cinemas in a town where there are currently none. The hopeful exhibitor has three main choices which we investigate below using the Dynamic Demand model: In this model, we assume that films are released at regular intervals, and the frequency of release lies outside the control of the exhibitor. The demand for each film is greatest when the film is released, and then decreases as time passes. When each subsequent film is released, demand for the first film drops suddenly, and then continues to fall at the original rate. The first drop is greatest; the following releases have less effect. A film's audience is usually built up during the first week of release, either as a result of distributors' marketing strategy or because of audience demand leading the supply. 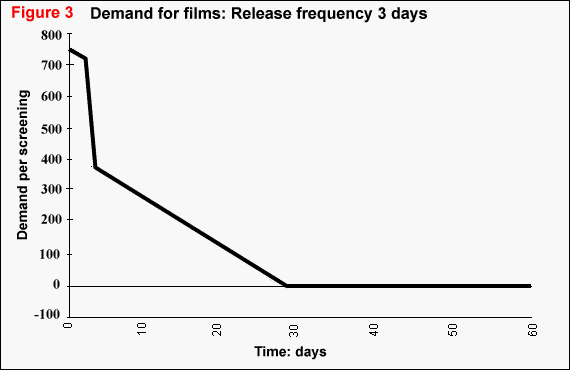We concentrate on the audience of a single screen, assuming that the film in question is neither arriving nor leaving a screen nearby. Figure 3 presents the resulting shape of the demand function for an individual film over time. The demand is the average number of people who wish to attend a single screening of the film. We assume that this pattern of demand is the same for all films(11).
 
 
The effect of release frequency on demand
 
We are interested in exploring the effect in the model of changing the assumed time between releases. In order to do this, we must make some assumptions about the effect that changing this parameter has on demand.
 
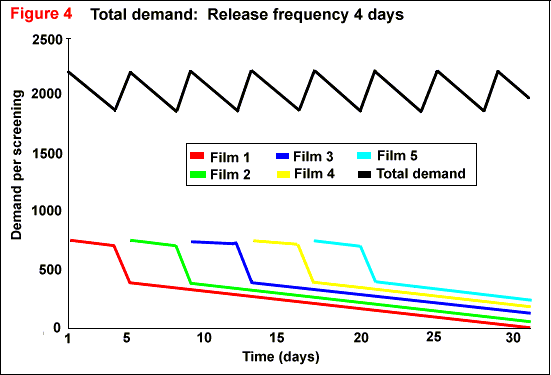
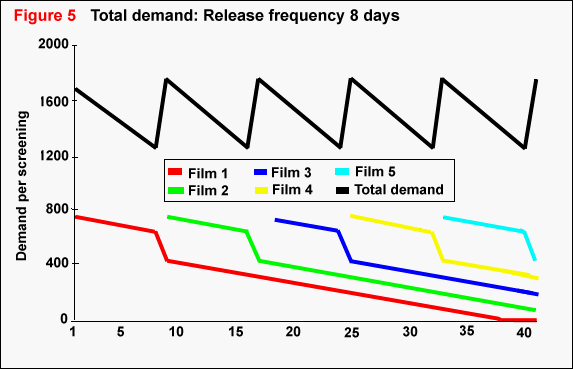
In our model, as release frequency increases, total demand at any time will increase. In other words, we assume that demand is to some extent driven by supply. However, this effect is not without limit: in the model, as the frequency increases, the reduction in demand for a film when the following films are released increases. Figures 4 and 5 show the demand for films, and total demand, with four and eight days between releases respectively.
 
Increasing the frequency of releases also decreases the length of time for which there is positive demand for any given film. If there are more films coming out per unit time, then interest in each film is sustained for a shorter period. Table 28 shows the duration of demand for different values of T, the time between releases.
 
 
 
 
 

  

Table 28 
Duration of demand for films
Time between releases (days)
Demand period for each film (days)
1
21
3
29
5
33
10
41
30
51
SOURCE: MEDIA Salles/London Economics
 
 
The cost of screens
 
We assume that there is a fixed cost of building screens, and that the marginal cost of an extra seat falls in the capacity range we are interested in.
 
There are economies of scale in building screens together on one site. Less land is needed, and less staff. Staff can be saved in administration, in selling confectionery, and in manning projectors, if the cinema is purpose-built so that all screens are served by a single projection room. While we assume that the costs per seat for any particular screen is the same, different assumptions have been used regarding fixed costs per screen. In this way we can analyze the effect on the number of screens built of the exhibitor exploiting the economies of scales by building a multiplex on one site.
 
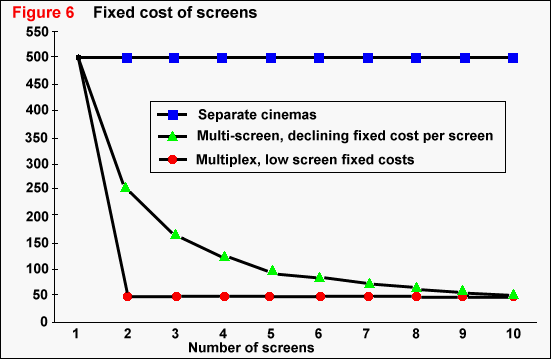
We do this by assuming a different pattern of fixed costs-per-screen in three cases: These three patterns for fixed costs for additional screens are shown in Figure 6.
 
By reducing the fixed cost element of the smaller screens, building on one site makes more screens profitable, and so more screens are built. This in turn means that overall attendance will be greater in the catchment area: the extra small screens will cater for the "tail" of the demand curve, those people who want to see the film towards the end of its release.
 
 
 
Results of the model
 
So far, our model has established that as more films are released per unit of time, the demand period associated with each film becomes shorter. We have also established that additional capacity has different costs in the three types of cinema analyzed.
 
Consider first the case of building only one screen. If extra capacity came at no cost, the best choice would be to build a screen large enough to hold the entire potential first night audience. The capacity utilisation of the screen would then decrease as interest in the film fell away, until a new film is released, attracting new demand. However, since there is a cost to building extra capacity, there is a trade-off between being able to accommodate the potential first night audience and the cost of empty seats during the latter period of the release. At the optimum capacity, the cinema will be full for a period at the beginning of the release, and will then empty gradually.
 
Given the characteristics of demand, the model calculates the optimal capacity for each screen, and the optimal number of screens. The latter is determined by adding screens until the smallest screen is not profitable. For example, if a sixth screen would not be profitable, the optimal number is 5.
 
At optimal capacity level, with this number of screens, there are two sources of excess demand: in the first period of release, because screen sizes are below the level of demand at the time of each new release; and in the tail of the demand curve, where it is not profitable to build a screen of any size to accommodate so few customers.
 
We now consider the effect of varying the demand and supply parameters of the model.
 
 
The effect of more frequent releases
 
Tables 29 and 30 show the effect of varying the frequency of releases. As releases become more frequent, more screens are built. This is because the "lifetime" (i.e. days of positive demand) of each given film decreases as more films are released in a period of time and demand is concentrated in the first days.
 
When there are 30 days between each new release (bottom row), only one screen is built, with a capacity of 640 seats. Demand for the film continues for a total of 51 days (see Table 28). However, it is not profitable to build a second screen to capture demand over the 20 days from day 31 to day 51 when demand drops from around 300 to 0. For 10 days, this second screen would be completely empty; the average level of attendance over 30 days would not justify a second screen. When there is a release every day, (row 1) seven screens are built. The capacity of the biggest (747) is higher because each new release is transferred to the next screen before demand has dropped significantly.
 
Table 29 
The Effect of Varying Release Frequency on the Optimal Number of Screens and Screen Capacities
 
Screen No: 
Optimal seat capacity by Screen
1
2
3
4
5
6
7
Time 
Between Releases  

(days) 
1
747
355
304
269
239
216
201
2
744
359
309
268
228
0
0
3
741
364
313
267
216
0
0
4
738
369
307
246
0
0
0
5
735
374
296
219
0
0
0
10
718
399
239
0
0
0
0
15
701
426
0
0
0
0
0
20
682
341
0
0
0
0
0
25
662
0
0
0
0
0
0
30
640
0
0
0
0
0
0
SOURCE: MEDIA Salles/London Economics
 
We can now show the effect on profits of building many screens compared to only one screen. If the exhibitor is constrained to build a maximum of only one screen then the optimal capacity is the capacity of the first screen in Table 29. In the second period the new release comes into this screen. By building only one screen the exhibitor therefore loses out on the profits from all the other screens which are profitable to build. There is a corresponding loss in attendances, since only the first part of the temporal demand curve is catered for. If the time between releases is 25 days or less, it is better to build more than one screen.
 
 Table 30 
Release Frequency and Screen Profit per Screening (£)
 
Screen No:
Profit by screen
1
2
3
4
5
6
7
  

  

Time Between Releases 

(days) 

 

 

 
1
1,902
497
339
231
141
73
29
2
1,866
496
338
215
95
0
0
3
1,830
496
337
198
49
0
0
4
1,794
495
305
122
0
0
0
5
1,758
495
257
31
0
0
0
10
1,578
493
23
0
0
0
0
15
1,400
493
0
0
0
0
0
20
1,222
165
0
0
0
0
0
25
1,044
0
0
0
0
0
0
30
867
0
0
0
0
0
0
SOURCE: MEDIA Salles/London Economics
 
 
 The effect of building screens on one site
 
One of the main purposes of the modelling exercise is to see what difference it makes to the number of screens built if all screens are built on one site, as against individual sites for each screen. We do this by varying our assumptions about the nature of the fixed cost of screens.
 
Table 31 shows the results for different release frequencies and different fixed screen- costs in the multiplex model. By building a multiplex instead of separate screens, more small screens become profitable. The number of screens built is therefore greater. There is little difference between the two formulations of multiplex fixed costs, since the cost for marginal screens is similar.
 
Table 31 
How the Optimal Number of Screens Varies with the Cost of Screens and Release Frequency
 

 
Screen fixed cost
High
Medium
Low
(a) Release period 10 days      
Separate sites
3
3
3
Multiplex, falling fixed costs
3
3
3
Multiplex, low fixed costs
3
4
4
(b) Release period 5 days      
Separate sites
4
4
4
Multiplex, falling fixed costs
6
6
6
Multiplex, low fixed costs
6
6
6
(c) Release period 3 days      
Separate sites
5
5
5
Multiplex, falling fixed costs
8
8
8
Multiplex, low fixed costs
8
8
9
SOURCE: MEDIA Salles/London Economics
 
However, the difference is greater, the greater the frequency of releases. When there are frequent releases, a significant reduction in fixed screen costs means that many more screens become profitable. If releases are less frequent, then only a few screens become profitable.
 
The increased number of screens means that more people come to see each film. The main source of excess demand, discussed above, lies in the tail of the demand curve. This excess demand is partly catered for by the extra small screens which become profitable if a multiplex is built.
 
 
Model 2: Random Demand for Films
 
Cinema attendances are hard to predict. For US films shown in the UK, the US success gives an indication of the likely success in the UK. In general, however, and even for US films, attendance is impossible to predict accurately before the film is released.

Let us assume that an existing cinema has a given number of seats. There are two films the cinema could take, a potential blockbuster, and a second film, which is expected to be less popular. The important questions for this hypothetical cinema are:

In this model, there is a minimum and maximum level of demand for each film which are known before the film is released. However, the actual level of demand for the film when it is released could be anywhere between these two extremes. The blockbuster is expected to have higher demand than the second film - the minimum and maximum are both higher for the blockbuster. We also assume there is some fixed cost to splitting the existing screen into two. Of course, if instead we consider building a cinema from scratch, then there may be less difference in cost between building one or two screens than if we imagine converting an existing single screen into a 2-screen. Even so, it will probably be more expensive to build a 300-seat screen and a 200-seat screen than a single 500-seat screen.
 
The profitability of splitting a single screen into two separate ones depends on a number of factors: In general terms, splitting a screen is profitable if it increases the rate of capacity utilisation of the cinema.
 
Capacity utilisation will increase, for example, if the overall capacity of the cinema is greater than the minimum level of demand for the blockbuster film. In this case there will be occasions in which a single screen would not be full. Splitting the screen would enable the cinema to show both films, attracting customers with different tastes and effectively increasing the demand facing the cinema.
 
However, taking an extreme case, if the overall capacity of the cinema is lower than the minimum demand of the blockbuster film, the cinema with a single screen would always have a full house by showing the blockbuster film, and there is therefore no incentive to split it into two.
 
Such a model shows that revenues can increase from splitting the screen for different levels of overall capacity. Gross profits increase up to the point where the combined minimum demand is large enough to fill always cinema capacity. Beyond this point, gross profits are constant.
 
Furthermore, gross profits from splitting the screen are larger the greater the overall capacity of the cinema. A larger capacity would in fact allow the cinema to take full advantage of the increase in demand generated by splitting the screen and showing two films.
 
Uncertainty in demand, however, has different effects on the relative profitability of cinemas of different sizes. This is because greater levels of uncertainty mean lower minimum values of demand, for a given average value. The final results depend on the relative size of demand with respect to overall cinema capacity.

 
Model 3: The Dispersion of Taste for Films
 
There are many films on release at any one time, and different films may appeal to different tastes; by having many screens, the multiplex can show more of the films which are on release at any one time.
 
Let us consider a cinema which has a local monopoly in a small town. There are a variety of films produced of different genres: action, horror, romantic, specialist etc. Different consumers prefer different types of film. In the model, this is represented by consumers tastes being distributed on a circle, with films at different points on the circle. A consumer then has to 'travel' to the film which most closely matches his or her preference. The total "cost" to the consumer of going to a film comprises two elements: how different the film is to the consumer's preferred type of film and the cost of admission.
 
There is a cost to showing additional films in the cinema: this is the cost of building and running more screens. The price of admission is the same for each screen. The cinema has to decide how many screens to build, and how much to charge for admission. The model then predicts, given the demand for films, and the cost of extra screens, how many screens should be built to maximise profit.
 
The model demonstrates that one benefit of multi-screen cinemas is the capacity to show films of different genres on one site, thereby capturing more demand than a single screen cinema. This applies in a small town, or in the suburbs of a city, where the overall level of demand is not sufficient to sustain more than one or two cinemas. In a city centre, however, it may not be this reason that drives the development of multi-screen cinemas, since there are usually individual cinemas that show films of a particular genre. The level of demand is high enough in the city centre to make these specialist cinemas economically viable.
 
In our model, the number optimal of screens increases as consumers become more fussy, or if demand for films in general increases, or if the cost of building additional screens falls.
 
 
Summary
 
The three models discussed in this section show that cinemas with many screens profit over single screen cinemas in many ways:

(11) In practice, demand for different films will be nowhere near the same, nor is it actually predictable in advance. This could be incorporated in a more sophisticated model by seeing what happens if we assume that initial demand is a random variable, with an expected value and a probability distribution. Uncertainty in demand is considered, even though within a static framework, in Section 3.2.